みなさん,こんにちは。
シンノユウキ(shinno1993)です。
最近,最適化問題に興味がでてきました。
これを利用して,健康的な食事パターンや食品構成表の自動作成なんかができないかなぁと妄想しています(ちなみに実際に活用もされているようです)。
最適化問題については「高校の時にちょっとやったかなぁ」という位の底辺レベルですので,0から勉強しなくてはなりません。とはいえ,私はそっち側の人間ではありませんので,「道具としてある程度使えたら良いかな」くらいの認識でおります。
調べてみると,Pythonを利用することで比較的簡単に実装できるということでした。なので根源的な理解は棚上げし,とりあえずやってみることにします。
今回はPythonライブラリ:PuLPを利用して最適化問題(そのうち線形計画問題)に挑戦してみようと思います。
では行きましょう!
線型計画法とは?
ある制約下で目的とする関数を最適化(最小もしくは最大)する変数の値を求める方法を数理計画法といい,そのうち制約や関数が線形の方程式で示されるものを線形計画法といいます。
栄養学の分野でも,最適な食事パターンや食事ガイドラインの策定等に利用されてきました(R)。
今回は線形計画法を用いた最適化について,Pythonライブラリの1つである「PuLP」を用いて簡単なものを実装してみます。
PuLPとは?
PuLPは,Pythonで無料で利用できるライブラリです。最適化問題の解決のために活用されます。線形計画法だけでなく,他の手法でも利用することができます。
公式ドキュメントは以下です:
食事問題
食事問題の概要
線形計画法を理解するために,まずは動かしてみることにします。今回は,私が直感的に問題を理解しやすい「食事問題」を題材としました。問題は以下のようなものになります:
問題)食品A,B,Cの3種類を組み合わせて摂取する。
栄養素摂取量を満たした上で,食費を最小限にできる摂取量を求める。
●食品
・食品A:価格=20, 栄養素1=22, 栄養素2=20, 栄養素3=10
・食品B:価格=12, 栄養素1=13, 栄養素2=30, 栄養素3=5
・食品C:価格=18, 栄養素1=17, 栄養素2=5, 栄養素3=12
●必要な栄養素摂取量
・栄養素1:200
・栄養素2:200
・栄養素3:100この場合,目的関数は食品Aの重量をXa(g),BをXb(g),CをXc(g)とした場合,以下のようになります:
【目的関数】
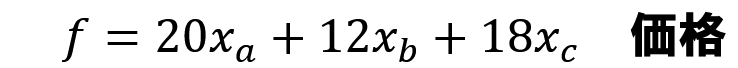
また満たさなければならない制約としては以下のようになります:
【制約条件】
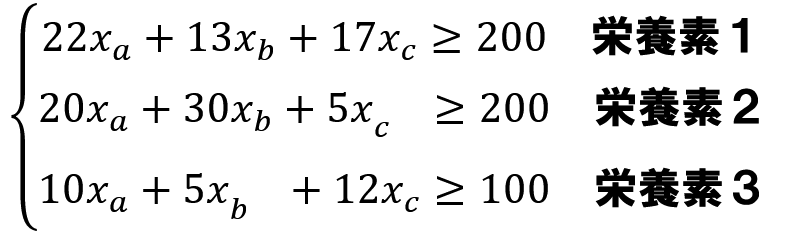
つまり,制約条件をすべて満たした上で,価格が最小になる食品の重量を算出すれば良いわけですね。
実際のコード
上記を解くコードをPuLPを使って書くと以下のようになります:
!pip install pulp
import pulp
# 問題の定義
problem = pulp.LpProblem(name="Diet", sense=pulp.LpMinimize)
# 変数の定義
A = pulp.LpVariable(name = "A", lowBound = 0, cat="Integer")
B = pulp.LpVariable(name = "B", lowBound = 0, cat="Integer")
C = pulp.LpVariable(name = "C", lowBound = 0, cat="Integer")
# 目的関数
problem += 20*A + 12*B + 18*C
# 制約条件の定義
problem += 22*A + 13*B + 17*C >= 200
problem += 20*A + 30*B + 5*C >= 200
problem += 10*A + 5*B + 12*C >= 100
# 解く
status = problem.solve()
print(pulp.LpStatus[status])
# 結果表示
print("Result")
print("A:", A.value())
print("B:", B.value())
print("C:", C.value())問題もシンプルですので,コードもシンプルかつ読みやすくなっていますね。
コードの解説
では,以下でコードを解説していきます:
①ライブラリのインストールとインポート
!pip install pulp
import pulpまずはPuLPをインストールして,それをインポートしています。
すでにPuLPをインストールしている方は一行目は不要です。
②問題の定義
#問題の定義
problem = pulp.LpProblem(name="Diet", sense=pulp.LpMinimize)ここでは線形計画問題を作成しています。
関数: lpProblemを用いることで問題を作成することが出来ます:
- name:問題の名前を指定します。今回は
"Diet"としました。この名前は本問題をlpファイルとして出力する際にも用いられます。 - sense:線形計画問題の目的を指定します。デフォルトは
"LpMinimize"です。最大の値を求めたい時はここを"LpMaximize"としてください。
③変数の定義
#変数の定義
A = pulp.LpVariable(name = "A", lowBound = 0, cat="Integer")
B = pulp.LpVariable(name = "B", lowBound = 0, cat="Integer")
C = pulp.LpVariable(name = "C", lowBound = 0, cat="Integer")ここでは変数を定義しています。
関数:LpVariableを利用することで変数を定義できます:
- name :変数名を指定します。
"A"のように文字列型で指定してください。 - lowBound:変数の値の下限を指定します。今回の場合は負の値はとらないので
0としました。 - upBound:今回は指定していませんが,変数に上限を設定する場合は指定します。
- cat:変数のカテゴリを指定します。デフォルトは
"Continuous"で,"Integer"や"Binary"も指定できます。今回は"Integer"を指定しました。
食品A,B,Cの重量をそれぞれ変数A,B,Cで定義しました。
④目的関数の定義
#目的関数
problem += 20*A + 12*B + 18*Cここでは目的関数を定義しています。
下記の目的関数をproblemに足した形になります。
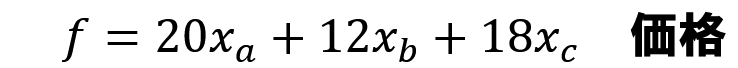
非常に簡単に定義できるのがわかりますね。
⑤制約条件の定義
#制約条件の定義
problem += 22*A + 13*B + 17*C >= 200
problem += 20*A + 30*B + 5*C >= 200
problem += 10*A + 5*B + 12*C >= 100ここでは制約条件の定義を行っています。
下記の制約条件をproblemに足した形になります。
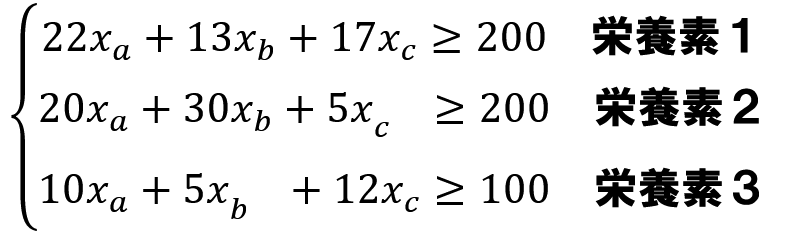
⑥問題を解く
#解く
status = problem.solve()
print(pulp.LpStatus[status])上記で問題を解いています。
関数:solveを実行すると,その実行結果が返されます。print(pulp.LpStatus[status])で実行した結果を表示しており,Optimalと表示されればOKです。
⑦結果の表示
#結果表示
print("Result")
print("A:", A.value())
print("B:", B.value())
print("C:", C.value())最後に,A,B,Cの3食品の重量を表示しています。
下記のように出力されていればOKです。
Result
A: 5.0
B: 3.0
C: 3.0まとめ
今回はシンプルな線形計画問題をPuLPを使って解いてみました。
次回はもう少し複雑なものに挑戦してみたい思います。
参考
今回の記事は以下の2つの記事を参考にさせていただきました。ありがとうございました。このような記事がインターネットに存在し,無料で手軽にアクセスできることをありがたく感じます。非常にわかりやすい記事でしたので,よろしければご参照ください:


