みなさん,こんにちは。
シンノユウキ(shinno1993)です。
今回は,性別や肥満度などに代表されるカテゴリデータの栄養統計についてみていきます.
仮説検定としては,以下の2つ
- ピアソンのカイ二乗検定
- フィッシャーの正確確率検定
をとりあげます.
では行きましょう!
検定の使い分けについて
はじめに,今回紹介する2つの統計手法の使い分けについて紹介します.この2つは,個人の好みで,どちらを使っても良い,というわけではありません.
単純化すると,
- ピアソンのカイ二乗検定→データ数の多い場合
- フィッシャーの正確確率検定→データ数の少ない場合
という風に使い分けます.
具体的には,分割表で期待度数5未満のセルが,全セルの20%以上ある場合はフィッシャーの正確確率検定を,そうでない場合はピアソンのカイ二乗検定を用います.
いきなり期待度数?という単語がでてきて,困惑する方もいらっしゃるかもしれません.以下の表で説明します.
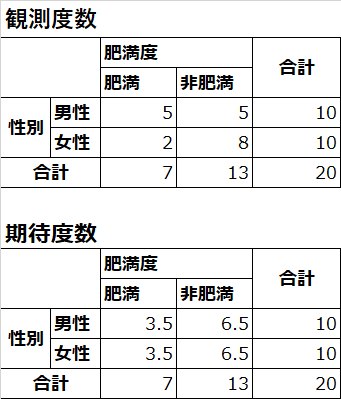
上側の表は,性別と肥満度のクロス集計です.男性の肥満の方は5人,女性の場合は2人という風に見ます.それぞれの列・行の合計も表示されてます.この値は実際に測定などをして導き出された値ですので,観察度数といいます.
これに対して,下側の表の値は期待度数です.このデータの場合,男性も女性も同じ10人です.それに対して,肥満者と非肥満者は男女合計でそれぞれ7人と13人います.つまり,男性にも女性にも,おなじ割合(7:13)で肥満者と非肥満者がいるのであれば,男女の両方とも,肥満者は3.5人,非肥満者は6.5人になるはずです.つまり,こうなることが期待されます.この度数のことを期待度数といいます.
先でちらっと説明しましたが,この期待度数が5未満のセルが20%以上であればフィッシャーの正確確率検定を,そうでない場合はピアソンのカイ二乗検定を用いるのでしたね.上の表でいえば,期待度数5未満のセルが50%(4セルのうち3.5が2つ)なので,フィッシャーの正確確率検定を用いる,ということになります.
そのため,基本的には人数が多ければ多くなるほど期待度数が5未満になるセルは少なくなるはずです.なので,人数が多い場合はピアソンのカイ二乗検定を少ない場合はフィッシャーの正確確率検定を用いましょうと単純化したのです.
データの読み込み
まずはデータを読み込みましょう.データは以下からダウンロードしてください:
ダウンロードしたデータを作業ディレクトリに格納し,以下のコードを実行しましょう:
df <- read.csv( "sample.csv", header = TRUE, sep = ",", skip = 0 ) df
以下のようなデータが表示されたらOKです:
sex. obes 1 male non-obes 2 male non-obes 3 male non-obes ・・・ 199 female non-obes 200 female non-obes
なお,データの読み込みについては,詳しくは以下をご参照ください:
ピアソンのカイ二乗検定
ではさっそく,ピアソンのカイ二乗検定を使ってみましょう.
ピアソンのカイ二乗検定を使うためには,まずは分割表を作成する必要があります.これはにはxtabsを使用します.以下のように使用します:
この分割表をピアソンのカイ二乗検定の関数の引数にします.なので,まずは分割表を作成してみましょう.コードは以下のようになります:
tab <- xtabs(~ df$sex + df$obes,
data = df)
tab
以下のように出力されるはずです:
df$obes df$sex non-obes obes female 60 26 male 76 38
変数:tabに分割表を挿入し,それを表示しています.
では,この分割表を使ってピアソンのカイ二乗検定を行ってみましょう.以下のように使用します:
では,実際に行ってみましょう.以下のようになります:
chisq.test(tab)
結果が以下のように表示されます:
Pearson's Chi-squared test with Yates' continuity correction data: tab X-squared = 0.097537, df = 1, p-value = 0.7548
p-value が0.754ですので,帰無仮説:観測された頻度分布と期待される頻度分布に差はないは棄却できません.つまり,性別と肥満に関係があるとは言えない,ということになります.
フィッシャーの正確確率検定
次に,フィッシャーの正確確率検定をRをで行う方法を紹介します.今回サンプルとしてるデータは十分に大きいので,フィッシャーの正確確率検定を行う必要はありませんが,例として今回は用いることにします.
フィッシャーの正確確率検定は以下の関数で行うことができます:
では,実際に使ってみましょう.以下のようになります.
fisher.test(tab)
結果は以下のように出力されます:
Fisher's Exact Test for Count Data data: tab p-value = 0.7596 alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 0.6060943 2.2136984 sample estimates: odds ratio 1.153022
こちらも p-value は0.7596ですので,帰無仮説が採用されます.結果はピアソンのカイ二乗検定と同様です.
まとめ
今回は,Rにおけるカテゴリデータの検定手法について解説しました.仮説検定としては,ピアソンのカイ二乗検定とフィッシャーの正確確率検定を取り上げました.ぜひ参考にしてください.
連載目次
- 【R×栄養統計】RとRStudioをインストールしよう
- 【R×栄養統計】四則演算と代表値の算出をやってみよう
- 【R×栄養統計】データの読み込み方法を習得しよう【TXT・CSV,・XLSX】
- 【R×栄養統計】性別と肥満度に関係があるか?カテゴリデータの栄養統計現在のページ
- 【R×栄養統計】正規分布しているか?正規性を確認する方法を紹介します
- 【R×栄養統計】男女でエネルギー摂取量に差はある?対応のない2群間の栄養統計
- 【R×栄養統計】栄養指導に効果はあった?対応のある2群間の栄養統計
- 【R×栄養統計】食べる速さでエネルギー摂取量に差がある?対応のない多標本の栄養統計
- 【R×栄養統計】多重比較を行う理由と使い分けを紹介|検定の多重性問題
- 【R×栄養統計】どの群間に差がある?対応のない多標本における多重比較


