【R×栄養統計】正規分布しているか？正規性を確認する方法を紹介します

みなさん，こんにちは。
シンノユウキ（shinno1993）です。

今回は正規性を確認する方法を紹介します．対象とするデータが正規分布に従うか否かは，解析手法を選ぶ際にも非常に重要になってきます．ここでは，正規分布の基本を確認しつつ，正規性を確かめる方法についても紹介します．

では行きましょう！

正規分布とは？
正規性を確認する方法
1. ①：ヒストグラムを描いて目視で確認
2. ②：シャピロ・ウィルク検定
まとめ
連載目次

正規分布とは？

正規分布は英語で normal distribution といい，その名の通り，この世にある最も一般的な分布の事を言います．ヒストグラムで書いてみると以下のような感じ．

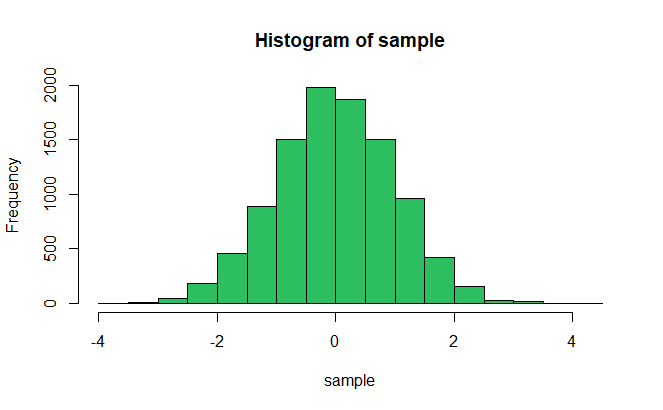
左右が対照で，真ん中が高く釣り鐘のような形をしています．分布が標準偏差に完全に従う場合，平均値と中央値と最頻値は同じになります．

また，平均値 ± 標準偏差の範囲に約68％が，平均値 ± ２×標準偏差の範囲に約95％のデータが収束するという性質もあります．学力テストなどに用いられる偏差値は，この正規分布の性質を利用しています．

統計解析手法には正規分布を仮定したものが多く存在します．また，正規分布を仮定することにより，分布がわかりやすく，また結果も解釈しやすくなりますので，しっかりと正規分布に従うか否か，また従わない場合はデータの変換などを試すことも必要になります．

一般的に，データの数が多ければ正規部分に従うとみなせるものが多くなりますが，特に栄養データを扱う場合，データが正規分布に従うとするかしないか微妙なものもあります．のでしっかりと確認する必要があります．以下で，正規性を確認する方法を紹介します．

正規性を確認する方法

まずは以下からCSVファイルをダウンロードし，変数dfに格納しておきましょう．

sample.csv

df <- read.csv(
  "sample.csv",
  header = TRUE  
)
df

①：ヒストグラムを描いて目視で確認

正規分布に従うか否かを確かめる方法として，まず行うべきなのは，ヒストグラムを描くことです．

これは統計的仮説検定でもなんでもありませんが，基本的にはしっかりとデータの分布をヒストグラムの形で確認することが重要なのです．

ヒストグラムは以下の式で描くことができます：

hist(ベクトル, col = 'カラー')

では，実際に書いてみましょう：

hist(df$energy, col = "green")

このデータだと，以下のようなヒストグラムが描けました：

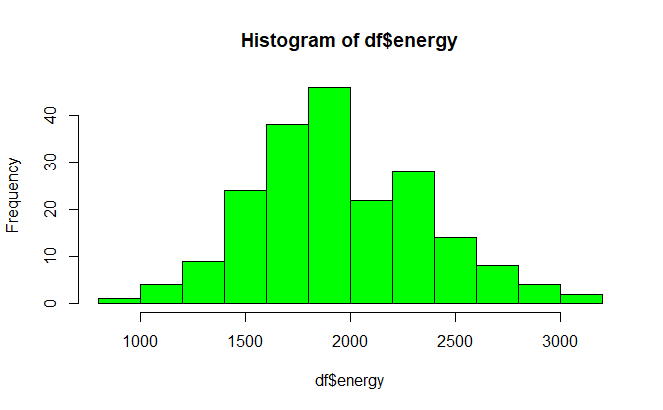
どうでしょう？先ほど例として示したヒストグラムほどではありませんが，悪くない分布だと思います．この分布だと，正規分布を仮定して分析を行っても良いように思います．

②：シャピロ・ウィルク検定

ただ，せっかくなので正規性を確認するための検定も紹介します．これはシャピロ・ウィルク検定と呼ばれるもので，その名の通り，シャピロとウィルクによって開発された手法です．以下のように使用します：

shapiro.test(ベクトル)

簡単ですね．では，先ほどダウンロードしたデータで試してみましょう：

shapiro.test(df$energy)

以下のような結果が出力されるはずです：

	Shapiro-Wilk normality test

data:  df$energy
W = 0.98765, p-value = 0.07979

この結果をみると，p = 0.798 となり，帰無仮説を棄却できませんでした．シャピロ・ウィルク検定の帰無仮説は「データが正規母集団から抽出されたものである」というもので，要するに正規分布に従うというものです．なので，それを棄却できない→正規分布に従うと言えないとは言えない，という少しややこしい言い方ですが，まぁ正規分布であるといってもいいという風な解釈ですね．

まとめ

今回は正規性を確かめる方法として，ヒストグラムで確かめる方法とシャピロ・ウィルク検定で確かめる方法の2つを紹介しました．他にも，コルモゴロフ・スミルノフ検定やQ-Qプロットなどの方法もありますが，とりあえず今回紹介した2つの方法を理解しておけば良いかと思います．

正規分布とは？

正規性を確認する方法

①：ヒストグラムを描いて目視で確認

②：シャピロ・ウィルク検定

まとめ

連載目次