みなさん,こんにちは。
シンノユウキ(shinno1993)です。
「今の食事をどれくらい変更したら最適な食事になるか」といった問題。
これには多くのアプローチがあるでしょうが,今回は線形計画法という数学的な手法を用いた食事最適化法について紹介します。
これには多くの事例がありますが,今回はその中からアメリカ人を対象にして行われた研究を紹介したいと思います。:
Gabriel Masset, Pablo Monsivais, Matthieu Maillot, Nicole Darmon, Adam Drewnowski, Diet Optimization Methods Can Help Translate Dietary Guidelines into a Cancer Prevention Food Plan, The Journal of Nutrition, Volume 139, Issue 8, August 2009, Pages 1541–1548, https://doi.org/10.3945/jn.109.104398
方法
概要
この研究では,線形計画法を用いて現在の食習慣をなるべく変更しないようにしながら,食事ガイドラインやDRIに適応させる食事計画を立案しています。なお「現在の食習慣」はアメリカの大学の教職員を対象に実施されたFFQによって測定されています。
線形計画法の目的条件
線形計画法において,目的関数は現在観察されている食品の摂取量と最適化された摂取量との差が最小になるように計画されています。これは以下のようになります:
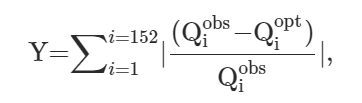
152種類の食品について,観察された摂取量から最適化された摂取量を差し引き,それを観察された摂取量で割った値の絶対値,これの総和が最小になるように設計されます。絶対値にする理由は乖離が多すぎても少なすぎてもダメなためです。また摂取量で割るのは,食品による摂取量の大小を標準化するために行っています。
ただし,このままだと線形計画法は使えません。絶対値を使うということは関数が線形にならないことを示しています。なので,正(Positive)を表すPと負(Negative)を表すNの2つの変数を導入することで,目的関数を以下のように定義しました:
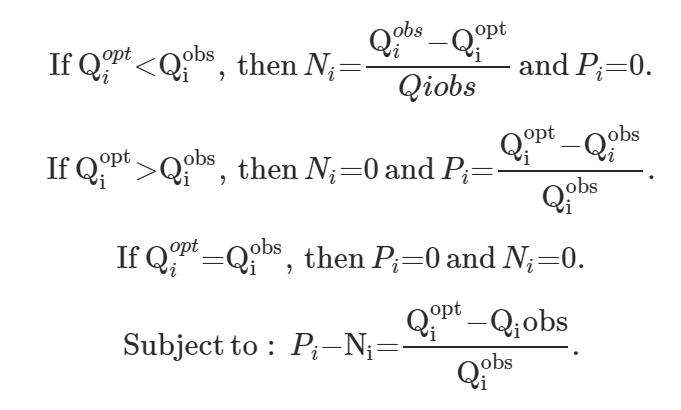
つまり,もし最適化された値の方が観察された値よりも小さければ,Nに観察値-最適値が,Pに0が代入されます。逆であればPに最適値-観察値が,Nに0が代入されます。もし同じであればどちらにも0が代入されます。そして,このPとNを足した数が当初求めたかった絶対値となります。以上より,新しい目的関数は以下になります:
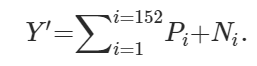
線形計画法の制限条件
次に,線形計画法の制限条件についてです。
本研究では次の2つのモデルを採用しており,それによって制限事項が異なります:
食事最適化法の2つのモデル
- がん予防のための食事ガイドライン(AICR)の遵守:エネルギー密度 1.25kcal/g,果物や野菜 600g以上・赤身肉 300g以下・食物繊維 25g以上・ナトリウム 2g未満
- 食事摂取基準(DRI)の遵守:PFCバランス(たんぱく質 10~35%,脂質 20~35%,炭水化物 45~65%),その他の栄養素
なお,エネルギー摂取量が同じ,食品群の摂取量が観察値の5%タイル以上かつ90%タイル値以下,食品の摂取量が観察値の90%タイル値以下という制限は2つのモデルで共通です。
結果
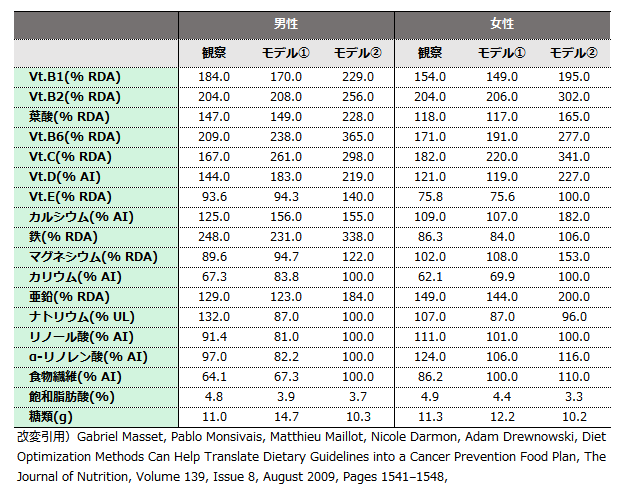
最適化を行った後の食品重量や食事コスト等を比較しています。必要な食事重量は大きく増加しており,特に女性ではモデル②で1kg近く増えてしまっています。さらに食事コストも増える傾向にあります。なお,MARはDRIをどの程度満たせているかを示すもので,モデル②では必然的に100%になります。
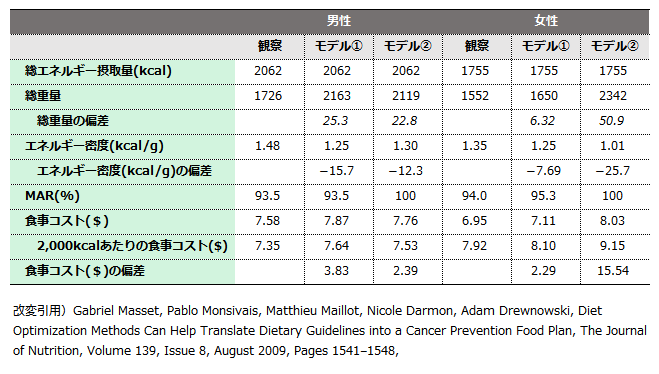
次に栄養素摂取量についてみてみます。モデル②では全ての栄養素摂取量で基準を満たしますが,水溶性ビタミンなどで摂取量がかなり多くなってしまっています。もともと基準値を遵守できていなかったVt.Eやカリウムについてはモデル①でも基準値に届いていませんでした。
この2つのモデルのうち,①の方は比較的簡単に達成できるようです。しかし,②の方は大きな食事内容の変更が必要になりました。一例として野菜類について見てみます:
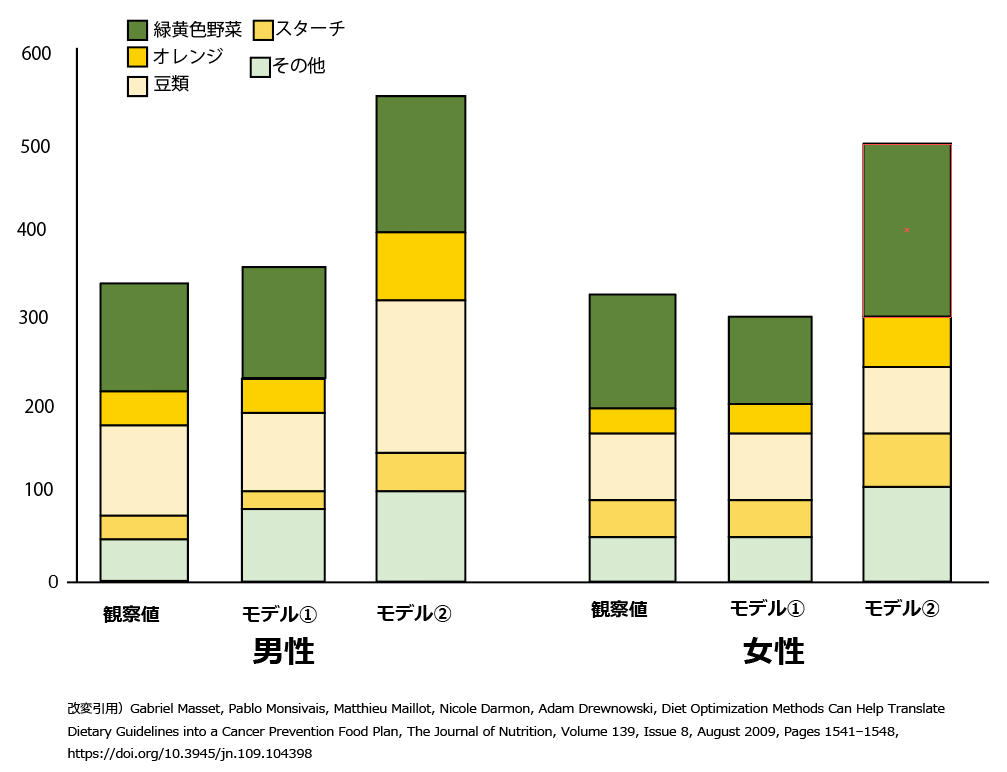
モデル①であれば,観察された値とほぼ同じで大きな変更は不要です。それに対してモデル②ですと200g程度の変更が必要になる計算になりました。
まとめ
今回の研究結果をまとめると以下のようになります:
- 食品をベースにしたモデルでは,比較的容易に達成可能な食品計画を提示できた
- DIRを達成するためのモデルでは,より多くの変更が必要だった。特にカリウムやビタミンEを摂取するために,他の摂取しやすい栄養素が過剰になりやすかった
- 数学的アプローチは栄養素をベースにした食事害ドライラインを食品ベースの食事ガイドラインに変換するために利用可能であることが示唆された
この研究はアメリカで実施されたものなので,このモデルがそのまま日本で利用できるかは不明です。それを知るためには,別の研究を参照する必要があります。次回はこちらの文献についてレビューしてみたいと思います。

